向量数据库语义检索

2025-04-22 • 5.1分钟 • 2.1千字

在聊向量数据库检索之前, 我们先来聊一下大模型目前的限制或者说缺陷. 不管是 GPT 还是 DeepSeek 都是有 token 的限制, 比如 gpt-3.5-turbo 的 token 长度限制是 4k, 那么意味着用户能输入大概 3000 多字供模型进行推理和处理, 如果超出这个长度那超出的部分可能就会被大模型“遗忘”,所以在给大模型聊天的时候可能聊着聊着他就好像忘了你之前对他的语义限制(忘记或者忽略你之前提到的点)。

可能有人说 GPT 是有记忆功能的, 或者分多次提交能突破 token 的限制, 其实这个想法是不正确的。不管你多次提交还是应用提供了记忆能力, 大致都是二次总结精简, 最终还是要提交给 LLM, 先不谈总结会不会丢失重要内容(LLM 理解偏差), 内容过多仍然出现 token 溢出, 所以限制依然是无法突破的, 这也是目前的复杂任务和处理大文本的难点.

除了 token 的限制, 还有就是大模型的训练成本和周期比较大, 训练结束后大模型的知识库就固化下来, 这也推动了 RAG 技术的兴起, 而 RAG 也是利用向量数据库来扩充 LLM 的知识库.

关键字检索(bm25) vs 语义检索

大多情况下把一整份资料扔个 LLM, 对 token 的消耗过于庞大, 这个时候其实只要把关键的资料部分给 LLM 基本就能达到目的。所以我们可以先把资料存到数据库, 然后检索出相关的部分再吐给 LLM。这里就不得不提到语义检索, 相比传统的关键字检索, 语义检索能 query 的含义来返回相关结果。举个例子,用户检索“我最喜欢的车“, 语义搜索侧重点在于符合你口味的车, 传统语义基于关键字, 大概率检索不到相关内容(比如喜欢车, 车爱好者等等).

这里就不得不提到向量数据库,向量数据库的核心思想是将文本转换成向量,然后将向量存储在数据库中,当用户输入问题时,将问题转换成向量, 然后在数据库中搜索最相似的向量和上下文,最后将文本返回给用户。

Text Embeddings

Text Embeddings 就是把文本数字化, 用于以机器易于理解的方式表示数据, 有很多用于构建文本嵌入的模型, 下面是一个简单的示例。

import os
from openai import AzureOpenAI
import numpy as np
from dotenv import load_dotenv
load_dotenv()

client = AzureOpenAI(
    api_version=os.getenv("AZURE_OPENAI_API_VERSION"),
    azure_endpoint=os.getenv("AZURE_OPENAI_ENDPOINT"),
    api_key=os.getenv("AZURE_OPENAI_API_KEY"),
)

text = 'the quick brown fox jumped over the lazy dog'
model = 'text-embedding-ada-002'

client.embeddings.create(input = [text], model=model).data[0].embedding

文本向量可以通过 OpenAI 的 text-embedding-ada-002 模型生成,图像向量可以通过 clip-vit-base-patch32 模型生成,而音频向量可以通过 wav2vec2-base-960h 模型生成. 这里我们用的是 text-embedding-ada-002 模型, 输出结果大致是:

[-0.00457075284793973,
 0.009826643392443657,
 -0.01506032980978489,
 -0.006350206211209297,
...
]

特征和向量化

向量化的过程, 就是用一个向量(可能是 N 维)来表示一个事物, 如果从理论角度出发, 我们会通过识别不同事物之间不同的特征来识别种类,例如分别不同种类的小狗, 就可以通过体型大小、毛发长度、鼻子长短等特征来区分。如下面这张照片按照体型排序,可以看到体型越大的狗越靠近坐标轴右边,这样就能得到一个体型特征的一维坐标和对应的数值, 从 0 到 1 的数字中得到每只狗在坐标系中的位置。

1d

然而单靠一个体型大小的特征并不够,像照片中哈士奇、金毛和拉布拉多的体型就非常接近,我们无法区分。所以我们会继续观察其它的特征,例如毛发的长短。

2d

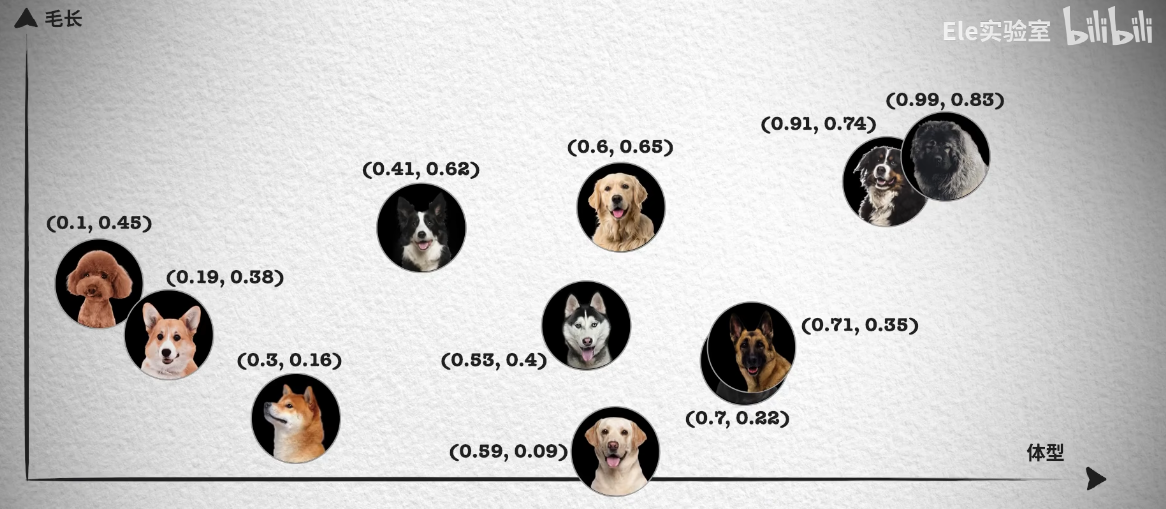
只要我们提供足够的特征就能更精确的表示一种狗狗, 当然用到的纬度可能也更高, 现在我们已经知道如何用向量表示事物了, 那如何解决检索或者说跟语义检索有什么关系呢？

相似性检索

我们只要计算两个向量的距离, 距离越小那相似度就越高, 说白了就是在坐标系里离的相对近。

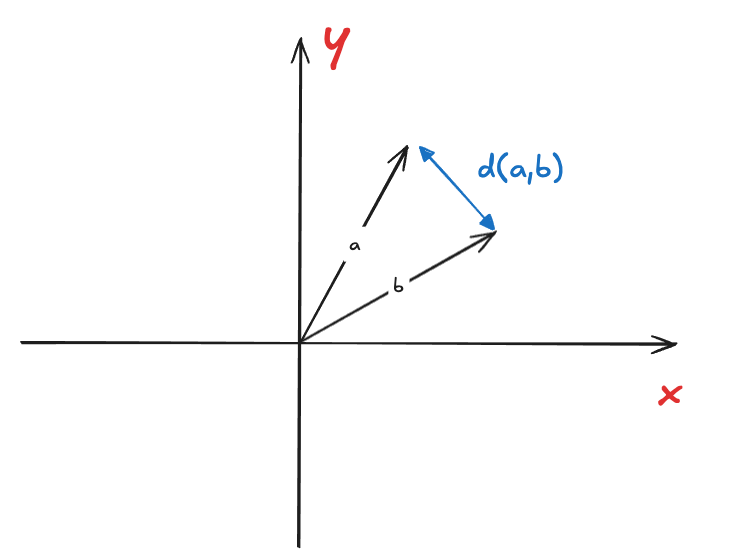
欧几里得距离（Euclidean Distance）

欧几里得距离是指两个向量之间的距离,即点到点的距离, 它的计算公式为：

d(A,B)=∑i=1n(Ai2−Bi2)d\left ( A, B \right ) = \sqrt{ {\textstyle \sum_{i = 1}^{n}\left (A^{2}_{i} -B^{2}_{i} \right ) } }

欧几里得距离在处理绝对距离比较重要的场景十分关键, 比如地图数据。

Euclidean Distance

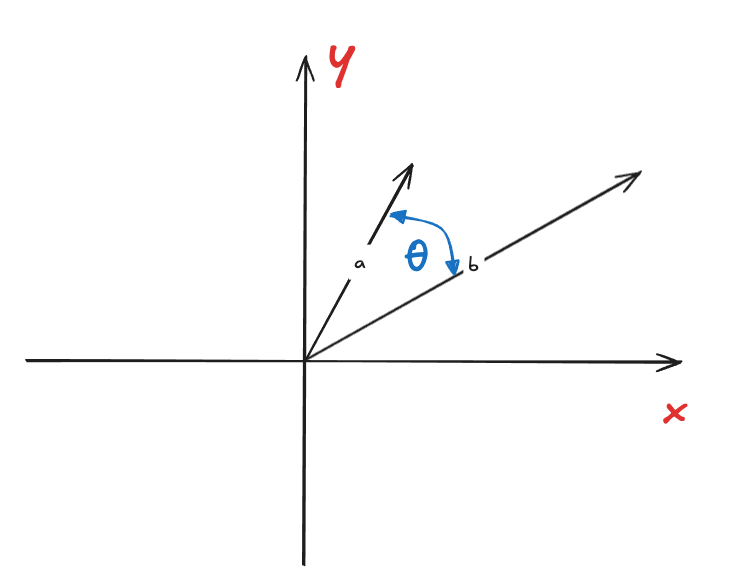
余弦相似度（Cosine Similarity）

余弦相似度侧重在夹角, 也就是说方向更重要。所以余弦相似度在处理文本、用户兴趣向量时比较对口, 词频不重要，词的组合/语义更重要. 计算公式可以从点积公式里得出。

a⋅b=|a||b|cosθ=ab|b|a\cdot b=\left | a \right | \left | b \right | \cos \theta = a_{b}\left | b\right |

然后直接变换得出余弦相似度:

cosθ=a⋅b|a||b|\cos \theta = \frac{a\cdot b}{\left | a \right | \left | b \right | }

Cosine Similarity

到这里我们可以大致知道语义化搜索用到的一些知识, 以及大致的实现方法。Text Embedding 后相当于向量化, 而此时只要找到某个向量附近的向量, 就找到了相似的向量. 当然采用距离还是夹角来找相似向量取决于需要使用的场景, 语义上的选用夹角比较合适。

检索效率

要找到最匹配的结果, 那肯定暴力检索最为精确. 但是千万上亿的向量用暴力检索肯定是不行的。

K-Means 算法

K-Means 是聚类算法，“聚类”的本质上是找到一组类, 这些类通常包含数据集中的所有对象。通常他有以下步骤:

Cosine Similarity

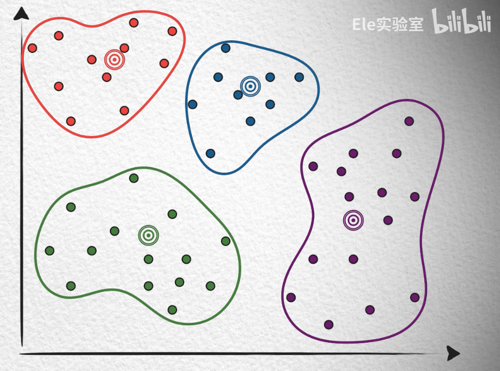
可以看出来聚类中心 k 小了搜索效率不高, k 大了占用更多的内存, 构建索引聚类时间变长, 但速度快。

Product Quantization (PQ)

我们用 K-Means 虽然一定程度上缓和了索引效率问题, 但是还有一个问题是内存占用问题.

假如有一个 128 维的向量, 那么他占用的内存是 128 * 32bit = 512 Byte, 那么 1 千万个向量就要占用 512B * 1kw = 5.8G 左右, 而实际场景中上亿的向量数量也不稀奇, GPT-4 甚至到了 1.76万亿, 纬度也达到了上万, 这个时候内存肯定是吃不消的。

在 K-Means 算法里我们已经找到了很多聚类(质心向量), 如果我们把每个分类里的向量用质心向量来表示, 那么就可以一定程度上起到了压缩作用(是不是类似图片压缩算法), 由于每个分类里的向量 是相似的, 我们只要为每个分类编号然后跟质心向量建立起联系即可(码本). 但是这样会引来额外的问题, 比如一个 128 维的向量可能最大需要 2642^64 个聚类(质心) 数量, 那这个时候码本的大小可能要比原始向量还要大, 本末倒置了。

解决方案就是把 128 维的向量分割成低纬的向量, 比如 8 个 16 维, 然后对子向量进行量化, 16 维的向量用到的聚类数量只有 256, 那加起来也就 8 * 256, 大大降低了聚类数量. 那如何还原呢？只要把 8 个 16 维合起来就能得到一样的效果，也就是 8 个结果的笛卡尔积.

TODO

总结

我们介绍了向量数据库用到的语义检索的部分原理和基本算法的实现, 也是在学习 Microsoft 的 generative-ai-for-beginners 时遇到的或者延伸到的问题。

References